The Concept of Linear Inequalities:

Linear inequalities are expressions in which the inequality symbols ‘’, ‘>’, ‘’, or ‘’ are used to compare any two values. These values might be numerical, algebraic, or a mix of the two. For example, 10<11, 20>17 are examples of numerical inequalities and x>y, y<19-x, x ≥ z > 11 are examples of algebraic inequalities (also called literal inequalities).

The following are the five symbols that are used to indicate linear inequalities in Maths:

Symbol Name	Symbol	Example
Not equal	≠	x ≠ 3
Less than	(<)	x 7 < √2
Greater than	(>)	1 10x > 2 16x
Less than or equal to	(≤)	y ≤ 4
Greater than or equal to	(≥)	-3 – √3x ≥ 10

Rules of Linear Inequalities in Maths

Addition, subtraction, multiplication, and division are the four types of operations performed on linear inequalities. Equivalent inequalities are linear inequalities. Both equality and inequality have their own set of norms. 

All of the principles listed below apply for inequalities involving less than or equal to () and larger than or equal to (). Let’s look at some of the key laws of inequality for all of these operations before learning how to solve linear inequalities.

Addition Rule of Linear Inequalities:

As per the rule, adding the same number to both sides of the inequality will result in equivalent inequality, which means the symbol will be the same.

If x > y, then x a > y a and if x < y, then x a < y a.

Subtraction Rule of Linear Inequalities:

As per the rule, removing the same number from both sides will result in equivalent inequality.

If x > y, then x − a > y − a and if x < y, then x − a < y − a.

Multiplication Rule of Linear Inequalities:

As per the rule, if we multiply the same number from both sides, it will result in equivalent inequality

If x > y and a > 0, then x × a > y × a and if x < y and a > 0, then x × a < y × a, Here, × is used as the multiplication symbol. 

Multiplication with a negative number on both sides of the inequality, on the other hand, does not yield an identical inequality unless the inequality symbol is likewise reversed.

If x > y and a < 0, then x × a < y × a and if x < y and a < 0, then x × a > y × a. 

Division Rule of Linear Inequalities:

As per the rule, if we divide both sides of an inequality with a positive integer, it results in an equivalent inequality, i.e. the inequality symbol will remain the same.

If x > y and a > 0, then (x/a) > (y/a) and if x < y and a > 0, then (x/a) < (y/a). 

Solving Linear Inequalities

It begins by isolating the variable from the constants. As per the inequalities rules, while we are solving multi-step linear inequalities, we must not forget to reverse the inequality sign when multiplying or dividing with any negative numbers.

Step 1: As per the law of inequality, simplify the inequality on both sides – LHS and RHS.

Step 2: If the inequality is strict, the solution for x is either less than or higher than the value given in the question. If the inequality isn’t a strict inequality, the solution for x is either less than or equal to, or higher than or equal to; the value reached as described in the question.

To further grasp the notion, let’s attempt to solve a linear inequalities example.

2x 3 > 7 

To solve this, we would follow the below-given steps:

2x > 7 – 3 ⇒ 2x > 4 ⇒ x > 2

Solving Linear Inequalities with Variable on Both Sides

Let us try solving linear inequalities with one variable by applying the concept we learned. Consider the following illustration.

3x – 15 > 2x 11

We proceed as follows:

-15 – 11 > 2x – 3x ⇒ – 26 > – x ⇒ x > 26

Solving Systems of Linear Inequalities by Graphing

The system of two-variable linear inequalities is of the form ax by > c or ax by ≤ c.  Inequalities’ indications can change depending on the set of inequalities provided. We need at least two inequalities to solve a system of two-variable linear inequalities. 

Let’s look at an example of how to solve a system of two-variable linear inequalities.

2y – x > 1 and y – 2x < -1 

We’ll start by plotting the specified inequalities on a graph. To do so, follow the instructions below:

-Substitute equal to = for the inequality sign, resulting in 2y – x = 1 and y – 2x = -1. We create dotted lines on the graph since the linear inequality is stringent.

-Check if the specified linear inequalities are satisfied by the origin (0, 0). If it does, darken the region that includes the origin on one side of the line. Shade the region on one side of the line that does not include the origin if the origin does not fulfil the linear inequality.

-The feasible zone that constitutes the solution of the system of linear inequalities will be coloured in common. The solution does not exist if there is no shared shaded region. The solution of the following system of linear inequalities is shown in pink in the graph below.

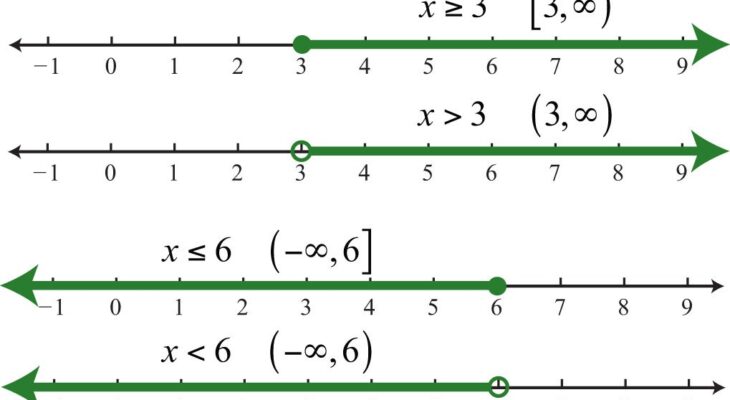
Graphing Linear Inequalities

Because the output offers the solution of one variable, linear inequalities with one variable are shown on a number line. As a result, just a number line is used to graph one-variable linear inequalities. 

Linear inequalities with two variables, on the other hand, are displayed on a two-dimensional graph since the output is the solution of two variables. As a result, a graph is used to graph two-variable linear inequalities.

Graphing One Variable Linear Inequalities

Let’s consider the below example.

4x > -3x 21

The solution, in this case, is simple.

4x 3x > 21 ⇒ 7x > 21 ⇒ x > 3

This can be plotted on a number line as:

This inequality may be satisfied by any point on the blue section of the number line. It’s worth noting that at point 3, we’ve drawn a hollow dot. This denotes that 3 is not included in the solution set (because the given inequality has a strict inequality). 

The blue section of the number line, according to the answer, satisfies the inequality. Let’s take another example of linear inequality:

3x 1 ≤ 7

We proceed as follows:

3x ≤ 7 – 1 ⇒ 3x ≤ 6 ⇒ x ≤ 2

We want to represent this solution set on a number line. Thus, we highlight that part of the number line lying to the left of 2

As shown in the figure, any number on the red section can fulfil the inequality. Hence it should be included in the solution set. At Point 2 on the number line, we’ve drawn a solid Dot showing that 2 is also a part of the solution set.

Important Results

1. If a, b ∈ R and b ≠ 0, then- 

(i) ab > 0 or a b > 0 ⇒ a and b are of the same sign. 

(ii) ab < 0 or a b < 0 ⇒ a and b are of opposite sign. 

1. If a is any positive real number, i.e., a > 0, then 

(i) | x | < a ⇔ – a < x < a 

     | x | ≤ a ⇔ – a ≤ x ≤ a 

(ii) | x | > a ⇔ x < – a or x > a 

     | x | ≥ a ⇔ x ≤ – a or x ≥ a

Conclusion

Therefore, we hope you understand to find out Linear Inequalities in Maths. Practice making the concepts more clear so that you can easily solve problems related to this topic.